code
DIRT: a deep inverse Rosenblatt transport method
DIRT is a MATLAB package that uses functional tensor trains and sparse polynomials to construct order-preserving, self-reinforced transport maps. The map has a composite form of \(T = T_0 \circ T_1 \circ \cdots \circ T_n\), in which each layer is a KR map constructed from a function approximation. Download MATLAB code from deep-tensor. Help files will be updated in May. Examples will be released under deep-tensor-examples in May.
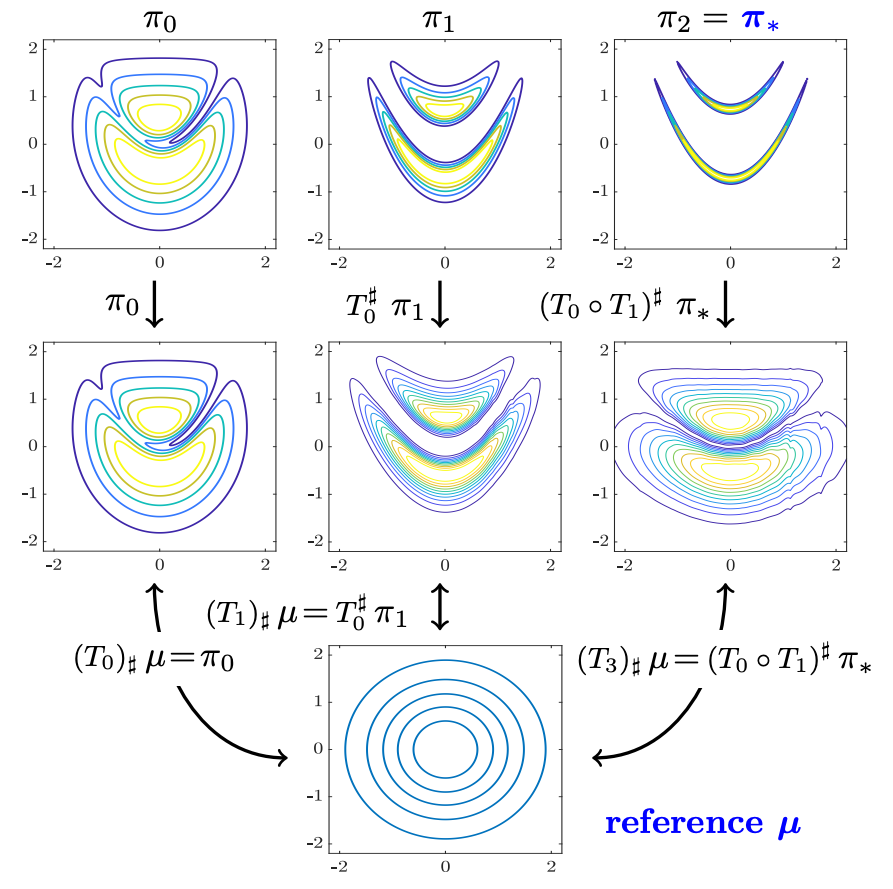
Suppose the log target density is \(\phi(x) := -\log \pi(x) = - 5(\log((1-x_1^2 + 100(x_2-x_1^2)^2) - 3)^2 + \cdots\)
>> phi= @(x) ...; % define potential function
>> base = ApproxBases(Legendre(30), BoundedDomain([-4,4]), d); % d = 2, define approximation space
>> kr = TTDIRT(phi,base,Tempering1()); % build DIRT using TT
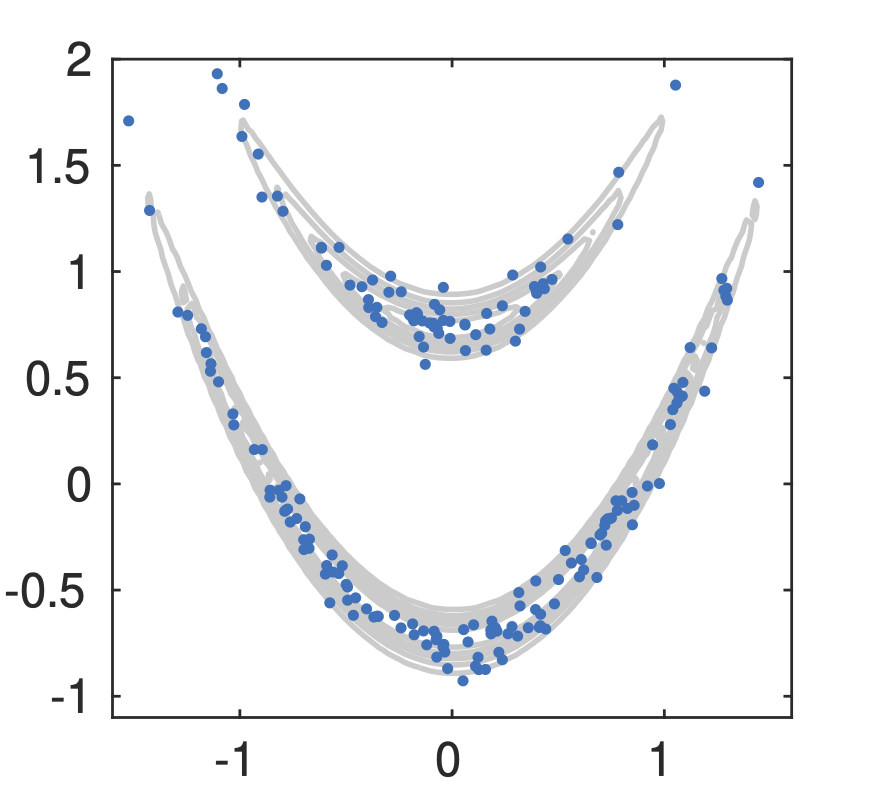
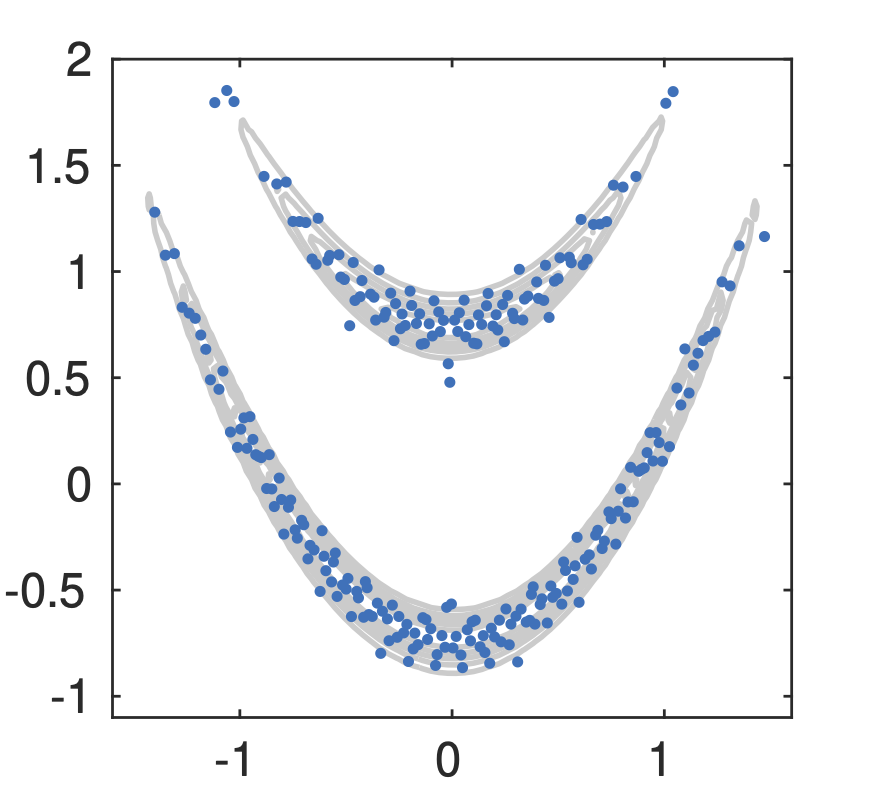
>> X = random(kr, 200); % random variable generation (left below)
>> X = sobol(kr, 200); % quasi Monte Carlo sample generation (right below) using Sobol sequence
 |  |
References:
Cui, T., & Dolgov, S. (2022). Deep composition of tensor trains using squared inverse Rosenblatt transports. Foundations of Computational Mathematics, 22(6), 1863–1922. https://doi.org/10.1007/s10208-021-09537-5
Cui, T., Dolgov, S., & Zahm, O. (2023). Scalable conditional deep inverse Rosenblatt transports using tensor trains and gradient-based dimension reduction. Journal of Computational Physics, 112103. https://doi.org/10.1016/j.jcp.2023.112103
Cui, T., Dolgov, S., & Scheichl, R. (2024). Deep importance sampling using tensor-trains with application to a priori and a posteriori rare event estimation. SIAM Journal on Scientific Computing, C1–C29. https://doi.org/10.1137/23M1546981
Cui, T., Dolgov, S., & Zahm, O. (2023). Self-reinforced polynomial approximation methods for concentrated probability densities.
Zhao, Y., & Cui, T. (2023). Tensor-based Methods for Sequential State and Parameter Estimation in State Space Models.
FastFIns
Fast Forward and Inverse problems solver (FastFIns) is a set of MATLAB code for accelerate the solution of inverse problems using likelihood-informed subspaces and data-driven model reduction. This package also contains a set of routines for defining high-order finite element discretization of PDEs.
A newer version of the code using fully object-oriented programming is under development. Download MATLAB code from fastfins.m.
References:
Cui, T., Martin, J., Marzouk, Y. M., Solonen, A., & Spantini, A. (2014). Likelihood-informed dimension reduction for nonlinear inverse problems. Inverse Problems, 30(11), 114015. https://doi.org/10.1088/0266-5611/30/11/114015
Spantini, A., Solonen, A., Cui, T., Martin, J., Tenorio, L., & Marzouk, Y. (2015). Optimal low-rank approximations of Bayesian linear inverse problems. SIAM Journal on Scientific Computing, 37(6), A2451–A2487. https://doi.org/10.1137/140977308
Cui, T., Marzouk, Y. M., & Willcox, K. E. (2015). Data-driven model reduction for the Bayesian solution of inverse problems. International Journal for Numerical Methods in Engineering, 102(5), 966–990. https://doi.org/10.1002/nme.4748
Cui, T., Marzouk, Y. M., & Willcox, K. E. (2016). Scalable posterior approximations for large-scale Bayesian inverse problems via likelihood-informed parameter and state reduction. Journal of Computational Physics, 315, 363–387. https://doi.org/10.1016/j.jcp.2016.03.055
Bardsley, J. M., Cui, T., Marzouk, Y. M., & Wang, Z. (2020). Scalable optimization-based sampling on function space. SIAM Journal on Scientific Computing, 42(2), A1317–A1347. https://doi.org/10.1137/19M1245220
Bardsley, J. M., & Cui, T. (2021). Optimization-based Markov chain Monte Carlo methods for nonlinear hierarchical statistical inverse problems. SIAM/ASA Journal on Uncertainty Quantification, 9(1), 29–64. https://doi.org/10.1137/20M1318365
Cui, T., & Tong, X. T. (2022). A unified performance analysis of likelihood-informed subspace methods. Bernoulli, 28(4), 2788–2815. https://doi.org/10.3150/21-BEJ1437
Zahm, O., Cui, T., Law, K., Spantini, A., & Marzouk, Y. (2022). Certified dimension reduction in nonlinear Bayesian inverse problems. Mathematics of Computation, 91(336), 1789–1835. https://doi.org/10.1090/mcom/3737