research
My research interests are broadly in computational mathematics for scientific machine learning and data science. I develop mathematically rigorous computational methods for statistical inverse problems, data assimilation and uncertainty quantification. These methods aim to optimally learn hidden structures and driven factors of complex mathematical models from data for issuing certified model predictions and making risk-averse decisions.
Selected research topics (outdated): likelihood-informed space, transport maps, model reduction, …
Likelihood-informed subspace
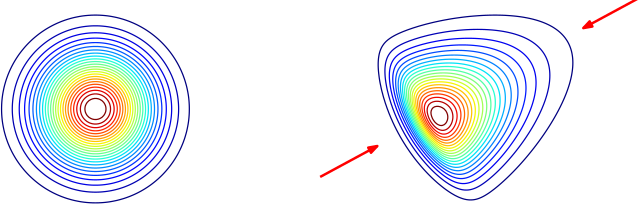
As a combined result of the smoothness of forward models, the regularity imposed by prior assumptions and the noise in incomplete data, the information update from the prior distribution (left figure) to the posterior distribution (right figure) may be confined to a relatively low-dimensional parameter subspace (indicated by red arrows).
We work on likelihood-informed subspace (LIS) to identify this subspace for breaking the curse of dimensionality. See my recent presentation for details. For more information, see the work on building dimension-robust MCMC samplers using LIS [1,2], its optimality in linear problems [3,4], and error analysis for general problems [5-8].
[1] Cui, T., Martin, J., Marzouk, Y. M., Solonen, A., & Spantini, A. (2014). Likelihood-informed dimension reduction for nonlinear inverse problems. Inverse Problems, 30(11), 114015. https://doi.org/10.1088/0266-5611/30/11/114015
[2] Cui, T., Law, K. J. H., & Marzouk, Y. M. (2016). Dimension-independent likelihood-informed MCMC. Journal of Computational Physics, 304(1), 109–137. https://doi.org/10.1016/j.jcp.2015.10.008
[3] Spantini, A., Solonen, A., Cui, T., Martin, J., Tenorio, L., & Marzouk, Y. (2015). Optimal low-rank approximations of Bayesian linear inverse problems. SIAM Journal on Scientific Computing, 37(6), A2451–A2487. https://doi.org/10.1137/140977308
[4] Spantini, A., Cui, T., Willcox, K., Tenorio, L., & Marzouk, Y. (2017). Goal-oriented optimal approximations of Bayesian linear inverse problems. SIAM Journal on Scientific Computing, 39(5), S167–S196. https://doi.org/10.1137/16M1082123
[5] Cui, T., & Zahm, O. (2021). Data-free likelihood-informed dimension reduction of Bayesian inverse problems. Inverse Problems, 37(4), 045009. https://doi.org/10.1088/1361-6420/abeafb
[6] Cui, T., & Tong, X. T. (2022). A unified performance analysis of likelihood-informed subspace methods. Bernoulli, 28(4), 2788–2815. https://doi.org/10.3150/21-BEJ1437
[7] Zahm, O., Cui, T., Law, K., Spantini, A., & Marzouk, Y. (2022). Certified dimension reduction in nonlinear Bayesian inverse problems. Mathematics of Computation, 91(336), 1789–1835. https://doi.org/10.1090/mcom/3737
[8] Cui, T., Tong, X. T., & Zahm, O. (2022). Prior normalization for certified likelihood-informed subspace detection of Bayesian inverse problems. Inverse Problems, 38(12), 124002. https://doi.org/10.1088/1361-6420/ac9582
Transport maps
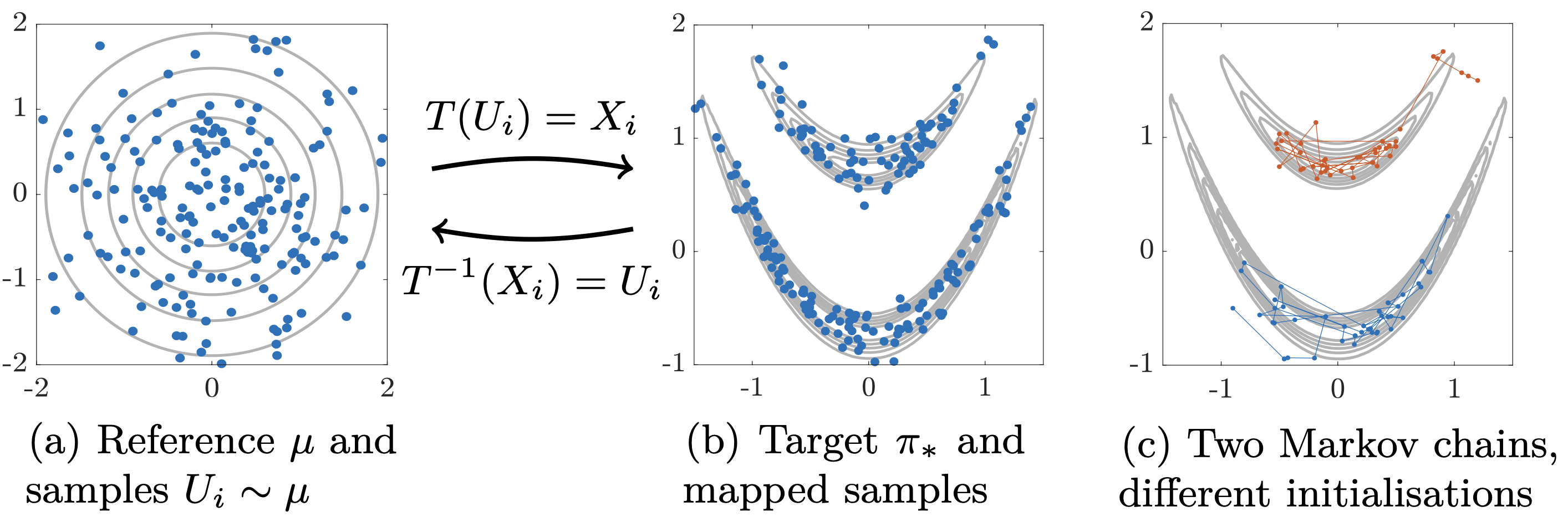
Characterising intractable high-dimensional probability distributions is one of the central tasks in data-science, computational physics, machine learning, and many other disciplines. The start of this dates back to the first general-purpose digital computer ENIAC, on which Metropolis, von Neumann, Ulam and other pioneers invented MCMC to simulate neutron diffusion. MCMC and its variants have become the workhorse for this task since then. The Markov construction makes MCMC methods challenging to parallelise and optimise. Transport maps offer a promising way to overcome MCMC’s limitations using order-preserving transforms that couple complicated target variables with analytically tractable reference variables.
We work on deep tensor-train and polynomial methods for building Knothe-Rosenblatt (KR) rearrangement [1,2]. This has been applied to build generative models with high-dimensional parameters and data [3], importance sampling for simulation data-driven rare events [4], and sequential learning in state-space models [5]. See the code and my presentation at the HDA workshop for some of these works.
We also extended the Stein variational transport maps of Liu and Wang by introducing Newton-type training algorithms and using LIS methods to design the reproducing kernels [6]. We developed optimisation-based transport maps for infinite-dimensional hierarchical inverse problems [7,8].
[1] Cui, T., & Dolgov, S. (2022). Deep composition of tensor trains using squared inverse Rosenblatt transports. Foundations of Computational Mathematics, 22(6), 1863–1922. https://doi.org/10.1007/s10208-021-09537-5
[2] Cui, T., Dolgov, S., & Zahm, O. (2023). Self-reinforced polynomial approximation methods for concentrated probability densities.
[3] Cui, T., Dolgov, S., & Scheichl, R. (2024). Deep importance sampling using tensor-trains with application to a priori and a posteriori rare event estimation. SIAM Journal on Scientific Computing, C1–C29. https://doi.org/10.1137/23M1546981
[4] Cui, T., Dolgov, S., & Zahm, O. (2023). Scalable conditional deep inverse Rosenblatt transports using tensor trains and gradient-based dimension reduction. Journal of Computational Physics, 112103. https://doi.org/10.1016/j.jcp.2023.112103
[5] Zhao, Y., & Cui, T. (2024). Tensor-train methods for sequential state and parameter learning in state-space models. Journal of Machine Learning Research, 25(244), 1–51.
[6] Detommaso, G., Cui, T., Marzouk, Y., Spantini, A., & Scheichl, R. (2018). A Stein variational Newton method. Advances in Neural Information Processing Systems, 9169–9179.
[7] Bardsley, J. M., Cui, T., Marzouk, Y. M., & Wang, Z. (2020). Scalable optimization-based sampling on function space. SIAM Journal on Scientific Computing, 42(2), A1317–A1347. https://doi.org/10.1137/19M1245220
[8] Bardsley, J. M., & Cui, T. (2021). Optimization-based Markov chain Monte Carlo methods for nonlinear hierarchical statistical inverse problems. SIAM/ASA Journal on Uncertainty Quantification, 9(1), 29–64. https://doi.org/10.1137/20M1318365
Model reduction and multilevel methods
[1] Cui, T., Marzouk, Y. M., & Willcox, K. E. (2015). Data-driven model reduction for the Bayesian solution of inverse problems. International Journal for Numerical Methods in Engineering, 102(5), 966–990. https://doi.org/10.1002/nme.4748
[2] Cui, T., Marzouk, Y. M., & Willcox, K. E. (2016). Scalable posterior approximations for large-scale Bayesian inverse problems via likelihood-informed parameter and state reduction. Journal of Computational Physics, 315, 363–387. https://doi.org/10.1016/j.jcp.2016.03.055
[3] Peherstorfer, B., Cui, T., Marzouk, Y., & Willcox, K. (2016). Multifidelity importance sampling. Computer Methods in Applied Mechanics and Engineering, 300, 490–509. https://doi.org/10.1016/j.cma.2015.12.002
[4] Cui, T., Fox, C., & O’sullivan, M. J. (2011). Bayesian calibration of a large-scale geothermal reservoir model by a new adaptive delayed acceptance Metropolis Hastings algorithm. Water Resources Research, 47(10). https://doi.org/10.1029/2010WR010352
[5] Cui, T., Fox, C., & O’Sullivan, M. J. (2019). A posteriori stochastic correction of reduced models in delayed-acceptance MCMC, with application to multiphase subsurface inverse problems. International Journal for Numerical Methods in Engineering, 118(10), 578–605. https://doi.org/10.1002/nme.6028
[6] Cui, T., Detommaso, G., & Scheichl, R. (2024). Multilevel dimension-independent likelihood-informed MCMC for large-scale inverse problems. Inverse Problems, 035005. https://doi.org/10.1088/1361-6420/ad1e2c
[7] Cui, T., De Sterck, H., Gilbert, A. D., Polishchuk, S., & Scheichl, R. (2024). Multilevel Monte Carlo Methods for Stochastic Convection–Diffusion Eigenvalue Problems. Journal of Scientific Computing, 99(3), 1–34.